PleistoDist

Island shape and distance metrics, normalised over Pleistocene time. A complete ground-up rebuild of PleistoDist for use with R.

Introduction

PleistoDist is a tool for visualising and quantifying the effects of Pleistocene-era sea level change on islands over time. This tool comes packaged as series of R functions, for generating maps of island extents for different Pleistocene-era sea levels, and calculating various inter-island and intra island distance and geomorphological metrics over time. This R package is a complete ground-up rebuild of the original PleistoDist, which was written as an ArcMap plugin.

Requirements

This package requires at least R v4.0.5 to function, and will automatically load the following dependencies:

• plyr
• dplyr.
• sf
• terra
• sp
• raster
• gdistance
• lwgeom
• tibble
• ggplot2
• ggspatial
• stats

Usage

To install and load this package in R, use the following commands:

devtools::install_github("g33k5p34k/PleistoDistR")
library(PleistoDist)

Inputs

You will need the following inputs in order to run PleistoDist:

• Bathymetry raster [.ASC] : PleistoDist requires an input bathymetry raster file in ASCII (.ASC) format to generate its outputs. Although PleistoDist should theoretically be able to use any type of ASCII-formatted bathymetric map as input, this tool has been tested specifically with data from the General Bathymetric Chart of the Oceans (GEBCO: https://www.gebco.net). Locality-specific bathymetric maps can be downloaded from https://download.gebco.net/.
• Source points [.SHP]: You will need to prepare a shapefile (.SHP format) of reference points that PleistoDist will use as sampling localities to calculate island shape parameters and inter-island distance matrices. The shapefile should have a column titled ‘Name’ with unique identifiers for each point, otherwise PleistoDist will default to using the FID identifiers of each point. The shapefile can be formatted in any map projection, since PleistoDist will reproject the shapefile to the user-specified projection for this analysis (see next point). Note, however, that the reprojection process might result in points close to the shoreline ending up in the sea, so do be mindful of that.
• Map projection [EPSG code]: Because of the Earth’s spherical shape, we need to apply a map projection to accurately calculate straight-line distances between points. Users should specify a projected coordinate system appropriate to the area being analysed using the projection’s associated EPSG code (https://epsg.org/home.html). Geographic coordinate system projections are not recommended as those will result in distance matrices calculated in decimal degrees rather than distance units.
• Time cutoff [kya]: PleistoDist calculates the average distance between islands over a specific period of time. Users will have to specify an upper time bound (in thousands of years [kya]) for their PleistoDist analysis, which can range from 0.1 kya to 3000 kya (i.e. 100 to 3,000,000 years ago). The lower time bound is fixed at the present day (0 kya). See the “How it works” section of the README file for more details.
• Binning Mode and number of intervals: PleistoDist simplifies the distance over time calculation by binning either time or sea levels into a number of equal user-specified intervals. This allows users to specify the coarseness of their analysis, with more intervals resulting in a more accurate and finer-grained analysis, although that will generate more output files and require a longer computational time. Binning by time is recommended for beginner users since it is more intuitive and more accurate as well. See the “General PleistoDist Workflow” section of the README file for more information on the difference between binning by time or by sea level.

General PleistoDist workflow

PleistoDist works by simplifying Pleistocene-era sea level change into discrete intervals, generating maps of island extents for each interval, calculating inter-island distances and metrics of island shape for each interval, and performing a weighted average for each metric across all intervals. This section provides a brief overview of the PleistoDist workflow, and how each metric is calculated.

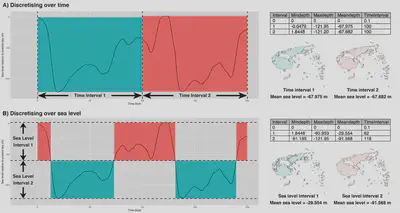
• Generating the interval file: The main role of the getintervals_time() and getintervals_sealvl() functions is to simplify reconstructed Pleistocene sea levels (by default from Bintanja and van de Wal, 2008) into a series of discrete interval bins. These intervals can be calculated in two different ways: either by binning over time, or by binning over sea level, as is illustrated in Figure 1. Theoretically, both methods should be equally accurate when the number of intervals is very high, but for intermediate numbers of intervals, binning by time is likely to be a better measure since it samples only one continuous section of the sea level curve per interval, and thus makes fewer assumptions about the shape of the curve for each interval. However, whether to bin intervals by time or sea level will likely vary depending on spatial and temporal scale, as well as the spatial context of the analysis, and as such both binning modes are made available in PleistoDist. The results of the binning process will be saved as an interval file in the output folder (see Figure 1), which will be used by subsequent modules for generating map outputs and calculating distance matrices. Each row in the interval file corresponds to one interval, and the first interval is always set at present day, with a mean sea level of 0 m and a time interval of 0.1 kya.

Figure 1: PleistoDist provides two different methods for discretising sea level change, either by time (A) or by sea level (B). Both methods should yield similar results when the number of intervals is very high, but will differ significantly for lower numbers of intervals. As this figure suggests, for a time cutoff of 200,000 years, 2 intervals not enough to capture the true variability of sea level change over this time period. The results of the binning process will be written as a table to the interval file in the output folder.

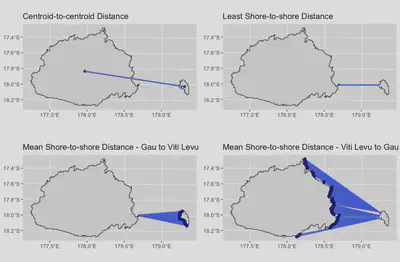
• Generating maps of island extents: The makemaps() function is responsible for generating map outputs based on the interval bins contained in the interval file. This module reprojects the input bathymetry raster into the user specified map projection using a bilinear resampling method, and generates raster and shapefile outputs of land extents based on the mean sea levels specified in the MeanDepth column of the interval file. This function generates maps in three formats: ESRI shapefile format, a flat raster format (with no topography), and a topographic raster format that preserves the original bathymetric elevations of each island pixel.

• Calculating island-to-island distances: PleistoDist provides 3 methods for calculating distances between islands. The pleistodist_centroid() function calculates the centroid-to-centroid distance, while pleistodist_leastshore() calculates the shortest shore-to-shore distance between islands. The last distance metric, pleistodist_meanshore() is slightly more complicated, and estimates the mean distance of every point on the source island shoreline facing the receiving island, to the receiving island shoreline. Because directionality matters in the case of the mean shore-to-shore distance, the resultant distance matrix is asymmetrical, and pairwise distances from large to small islands will generally be greater than from small to large islands. The mean shore-to-shore distance estimation method allows us to account for differences in shoreline availability between pairs of islands. For each pairwise combination of source points provided by the user, PleistoDist selects the landmasses corresponding to the pair of points, and calculates the two distance measures between the landmasses. If both points are on the same island for that particular interval, a distance of 0 is returned. And if one or both points are underwater during that particular interval, a value of NA is returned. Distance matrix outputs from this module are stored in the output folder.

Figure 2: PleistoDist calculates three different distance measures between islands: the centroid-to-centroid distance, the least shore-to-shore distance, and the mean shore-to-shore distance illustrated here with the Fijian islands of Viti Levu (left) and Gau (right). Note how the inter-island distances are asymmetric for the mean shore-to-shore distance.

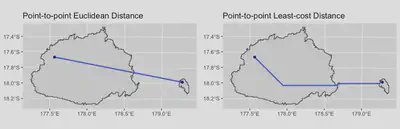
• Calculating point-to-point distances: Unlike island-to-island distance metrics, which considers entire islands as the fundamental unit for calculating distances, the point-to-point distance functions pleistodist_euclidean() and pleistodist_leastcost() calculate pairwise distances between the source points provided by the user (Figure 3). The function pleistodist_euclidean() calculates the Euclidean distance between points (which is invariant over time and therefore only calculated once), while the pleistodist_leastcost() function calculates the least cost distance between points for each interval (Figure 3). The resistance surface used for calculating the least cost distance is essentially a rasterised version of the shapefile for that interval, with areas above sea level assigned a resistance value of 1, and areas underwater assigned a resistance value of 999,999. The least cost distance should thus minimise the amount of overwater movement between points.

Figure 3: PleistoDist calculates two different distance measures between source points: the Euclidean distance between points (as the crow flies, invariant across all intervals), and the least cost distance (which minimises overwater movement), illustrated here with the Fijian islands of Viti Levu and Gau.

• Calculating island area, perimeter, and surface area: In addition to calculating inter-island distances, PleistoDist can also calculate the shapes of islands over Pleistocene time. The three functions, pleistoshape_area(), pleistoshape_perimeter(), and pleistoshape_surfacearea() are pretty self-explanatory, and they calculate the shape parameters of islands as identified by the user-provided points shapefile, for each time/sea level interval defined in the interval file, as well as the weighted mean of each parameter based on the duration of each sea level/time interval. PleistoDist will return a value of NA if the island is below sea level for that particular interval. Users can also use the pleistoshape_all() function to calculate all three shape parameters simultaneously instead of running each subsidiary function in succession, which should save a fair bit of computational time.

• Estimating net migration between islands: MacArthur & Wilson (1967) describe a simple model for estimating the number of propagules dispersing between two islands, as given by the equation: $$ n_{(1\rightarrow2)} = \frac{2\tan^{-1}(w_2/2d)}{360}\times \alpha A_{1}e^{(-d/\lambda)} $$ where $n_{1\rightarrow2}$ is the number of propagules of a particular species successfully dispersing from island 1 to island 2, w₂ is the width of island 2 relative to island 1, d is the distance between the two islands, α is the population density of the propagule population on island 1, A₁ is the area of island 1, and λ is the mean overwater dispersal distance of the propagule. While this equation is difficult to solve since it requires estimates for both α and λ, if we take the ratio of $n_{1\rightarrow2}$ to $n_{2\rightarrow1}$ – the net migration between islands 1 and 2 – we can cancel out both the α and the exponential terms, and reduce the relationship to $$\frac{n_{(1\rightarrow2)}}{n_{(2\rightarrow1)}}=\frac{\tan^{-1}(w_{2}/2d)A_{1}}{\tan^{-1}(w_{1}/2d)A_{2}}$$ which can easily be solved using the outputs generated by PleistoDist. As such, if there is a net movement of propagules from island 1 to island 2, $\frac{n_{(1\rightarrow2)}}{n_{(2\rightarrow1)}}>1$, whereas if there is a net movement of propagules from island 2 to island 1, then $\frac{n_{(1\rightarrow2)}}{n_{(2\rightarrow1)}}<1$. The net inter-island migation ratio can be estimated using the function pleistodist_netmig(), which automatically checks to see if the appropriate distance and shape matrices exist, and calculates the net inter-island migration for each time/sea level interval as specified in the interval file, and calculate a weighted mean net migration ratio across all intervals. Note that since the mean shore-to-shore distance matrix is asymmetrical, and we assume that the inter-island distance is symmetrical for this particular calculation, PleistoDist will use as d the mean of $d_{(1\rightarrow2)}$ and $d_{(2\rightarrow1)}$.

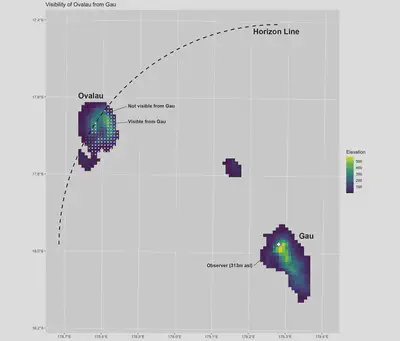
• Estimating island visibility: Inter-island dispersal can also be affected by the visibility of a destination island relative to an observer on an origin island. PleistoDist therefore provides a rudimentary way of estimating inter-island visibility using the function pleistodist_visibility(). This function works by first estimating the horizon distance of the observer point, taking into account both the ground elevation of the observer as well as the height of the observer above the ground, using the equation: $$\text{horizon distance}=R_{e} \times \sec^{-1}(1+\frac{h_{\text{total}}}{R_{e}})$$, where $h_{\text{total}}$ is the sum of the ground elevation and the height of the observer above the ground, and $R_{e}$ is the Earth’s radius for that particular inter-island great circle arc, accounting for sea level change, which can be approximated by the equation $$R_{e}=\text{sea level relative to present day}+\frac{a(1-e^{2}\cos^{2}\phi\cos^{2}\theta)^{\frac{3}{2}}}{(1-e^{2}[1-\sin^{2}\phi\cos^{2}\theta])^{\frac{1}{2}}}$$, where $a$ is Earth’s equatorial radius, $e^{2}$ is the squared eccentricity of Earth. $\phi$ the approximate azimuthal angle between the line connecting the observer and the destiation island and Earth’s North-South axis, and $\theta$ the parametric latitude of the observer. If the destination island falls within the radius of the horizon distance, PleistoDist calculates whether the horizon line intersects with the destination island (Figure 4). To account for the occluding effects of mountains and other geographical features, the function then performs a viewshed analysis to estimate the area of the island that is within direct line of sight from the observer (Figure 4). Do note, however, that due to the sampling method applied for the viewshed analysis, the calculated visible island area is likely to vary across multiple runs, so it’s best to treat the outputs of this function as an estimate rather than an absolute value. Note also that this function is unable to account for visibility-reducing weather effects such as fog, haze, or mist.

Figure 4: PleistoDist estimates the visibility of a destination island relative to an observer on an origin island by calculating the horizon line (which defines the theoretical maximum viewing distance relative to the observer), and performing a viewshed analysis to estimate the visible non-occluded area of the destination island.

Limitations

PleistoDist assumes that the bathymetry of the area of interest is constant throughout the time period being modelled. This is an important assumption to bear in mind since bathymetry can be affected by tectonic and volcanic activity. In the provided example of the Fijian archipelago, for instance, the island of Taveuni (see Figure 2) is likely to have emerged around 700,000 years ago (Cronin & Neall, 2001), so analyses of Taveuni with a cutoff time close to and exceeding 700 kya are unlikely to provide meaningful results. In addition, PleistoDist is unable to account for the effect of proximate ice sheets on the bathymetry and sea level of the area of interest, and is thus likely to be less accurate at very high or very low latitudes. It is also possible that the default global sea level reconstruction used in the vanilla version of PleistoDist may not be accurate for particular areas of interest, in which case users are advised to use a more accurate sea level reconstruction specific to the area of interest, bearing in mind to be aware of the column names in the new sealvl.csv file.

Further modifications/extensions

Advanced users should be able to modify the PleistoDist source code to meet their specific needs. Here are some suggestions:

• Sea level reconstruction: By default, PleistoDist uses the Pleistocene sea level reconstruction of Bintanja & van de Wal (2008), which is based on an inverse model using the ratio of marine Oxygen-18 to Oxygen-16 isotopes. This sea level reconstruction is stored as a pre-loaded R variable, and can be replaced with your preferred sea level reconstruction (e.g. from Spratt and Lisiecki, 2016). If you do swap out the sea level reconstruction, be sure to check and modify the getintervals.R file to make sure that this doesn’t break PleistoDist.
• Time lower bound: Vanilla PleistoDist fixes the lower time bound at the present day. Setting a different lower time bound should be relatively simple and can be achieved by modifying the getintervals.R file.

References

• Bintanja, R., & van de Wal, R. S. W. (2008). North American ice-sheet dynamics and the onset of 100,000-year glacial cycles. Nature, 454(7206), 869–872. https://doi.org/10.1038/nature07158
• Cronin, S. J., & Neall, V. E. (2001). Holocene volcanic geology, volcanic hazard, and risk on Taveuni, Fiji. New Zealand Journal of Geology and Geophysics, 44(3), 417–437. https://doi.org/10.1080/00288306.2001.9514948
• Darwell, C. T., Fischer, G., Sarnat, E. M., Friedman, N. R., Liu, C., Baiao, G., Mikheyev, A. S., & Economo, E. P. (2020). Genomic and phenomic analysis of island ant community assembly. Molecular Ecology, 29(9), 1611–1627. https://doi.org/10.1111/mec.15326
• MacArthur R. H., & Wilson E. O. (1967). The Theory of Island Biogeography. Princeton, N.J.: Princeton University Press, 203 p.
• Spratt, R. M., & Lisiecki, L. E. (2016). A Late Pleistocene sea level stack. Climate of the Past, 12(4), 1079–1092. https://doi.org/10.5194/cp-12-1079-2016